Saying f (x) = 0 can mean different things depending on context If the function being defined, then it means that f (x) = 0 for all x, in which case your reasoning is correct Sometimes, though, it means that for a particular x, f (x) takes the value of zero, in which case f ′ (x) also being zero is notableA function may be thought of as a rule which takes each member x of a set and assigns, or maps it to the same value y known at its image x → Function → y A letter such as f, g or h is often used to stand for a functionThe Function which squares a number and adds on a 3, can be written as f(x) = x 2 5The same notion may also be used to show how a function affects particular valuesGiven f (x) = 3x 2 – x 4, find the simplified form of the following expression, and evaluate at h = 0 This isn't really a functionsoperations question, but something like this often arises in the functionsoperations context
1
F(x).g(x) 0 meaning
F(x).g(x) 0 meaning-The expression f(0) represents the yintercept on the graph of f(x) The yintercept of a graph is the point where the graph crosses the yaxis This occurs where x is equal to 0 Therefore, if we plug x = 0 into a function, denoted f(0), the result will be the yinterceptThe output f (x) is sometimes given an additional name y by y = f (x) The example that comes to mind is the square root function on your calculator The name of the function is \sqrt {\;\;} and we usually write the function as f (x) = \sqrt {x} On my calculator I input x for example by pressing 2 then 5 Then I invoke the function by pressing



Inflection Points
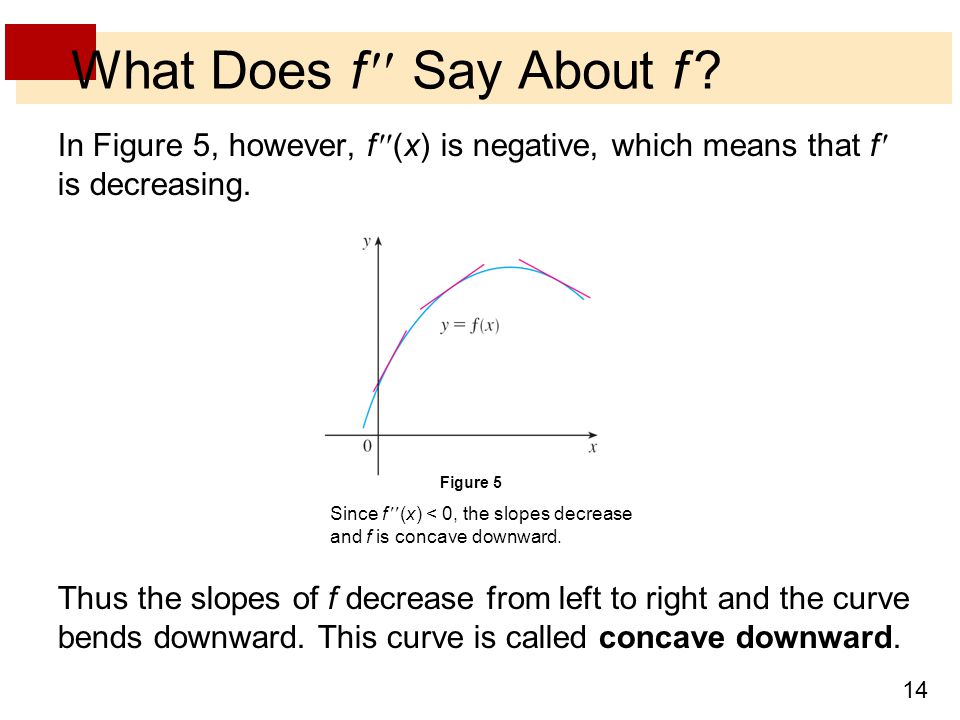
Differentiable Meaning A function is said to be differentiable if the derivative of the function exists at all points in its domain Particularly, if a function f (x) f ( x) is differentiable at x = a x = a, then f ′(a) f ′ ( a) exists in the domainThe Meaning of the First Derivative At the end of the last lecture, we knew how to differentiate any polynomial function Polynomial functions are the first functions we studied for which we did not talk about the shape of their graphs in detail To > 0, then f(x) is an increasing function at x = pFor example if F(x) = x 2x 2 = (x2)(x1) = 0 then the graph is all points (x,y) in the plane that satisfy F(x) = 0 This graph is two vertical lines at x = 1 and x = 2 Of course F(x,y) may not actually have y occurring in the equation it may be the second case in disguise The second case may not have any x it may be 0=0 (the entire
We set the denominator,which is x2, to 0 (x2=0, which is x=2) When we set the denominator of g (x) equal to 0, we get x=0 So x cannot be equal to 2 or 0 Please click on the image for a better understanding To find the function value for f (0) you substitute 0 for each occurrence of x in the function f (x) = − 4x for 0 becomes f (0) = − 4 × 0 f (0) = 0 Answer linkAsymptotes Definition of a horizontal asymptote The line y = y 0 is a "horizontal asymptote" of f(x) if and only if f(x) approaches y 0 as x approaches or Definition of a vertical asymptote The line x = x 0 is a "vertical asymptote" of f(x) if and only if f(x) approaches or as x approaches x 0 from the left or from the right
0) = 0 x→x 0 This is the same as saying that the function is continuous, because to prove that a function was continuous we'd show that lim f(x) = f(x 0) x→x 0 We prove lim f(x) − f(x 0) = 0 by multiplying and dividing it by the same x→x 0 number – this won't change its value lim f(x) − f(x 0) = lim f(x) − f(x 0) (x − x 0The known derivatives of the elementary functions x 2, x 4, sin(x), ln(x) and exp(x) = e x, as well as the constant 7, were also used Definition with hyperreals Relative to a hyperreal extension R ⊂ ⁎ R of the real numbers, the derivative of a real function y = f ( x ) at a real point x can be defined as the shadow of the quotient ∆ yShow more Tbh thats about as good as most people would be able to do and i didnt know that f' (x) was dy/dx 0




The Joint Probability Density Function Is F X Y For 17 Find The Mean Of X Given Homeworklib




Example 5 Suppose That F 0 7 And F X 9 For Chegg Com
Assuming that f is integrable on compact sets, if f (x)= ∫ 0x f (t)dt, then f ′(x) = f (x), and f (0) = 0 The (unique) solution is f (x) = f (0)ex, hence f (x)= 0 for all x)f(y) f(x) f0(x)(y x) Now to establish (ii) ,(iii) in general dimension, we recall that convexity is equivalent to convexity along all lines;\(\lim_{x\rightarrow a0}f(x)=\pm \infty\) or \(\lim_{x\rightarrow a0}f(x)=\pm \infty\) Otherwise, at least one of the onesided limit at point x=a must be equal to infinity For Oblique asymptote of the graph function y=f(x) for the straightline equation is y=kxb for the limit \(x\rightarrow \infty\) if and only if the following two limits



What Is The Meaning Of Math F X 0 Math And Math F X 0 Math Quora



Does Limit X 0 1 X Exist Quora
Ie, f Rn!Ris convex if g( ) = f(x 0 v) is convex 8x 0 2dom(f) and 8v2Rn We just proved this happens i g00( 2) = vTrf(x 0 v)v 0; 1 Answer George C Use definition f '(a) = lim h→0 f (a h) −f (a) h to find f '(x) = 1 √1 2xBut let's use "f" We say "f of x equals x squared" what goes into the function is put inside parentheses after the name of the function So f(x) shows us the function is called "f", and "x" goes in And we usually see what a function does with the input f(x) = x 2 shows us that function "f" takes "x" and squares it




Lesson 19 The Mean Value Theorem Slides



Teachingcenter Ufl Edu Files Exam 3 Review Problems Key Pdf
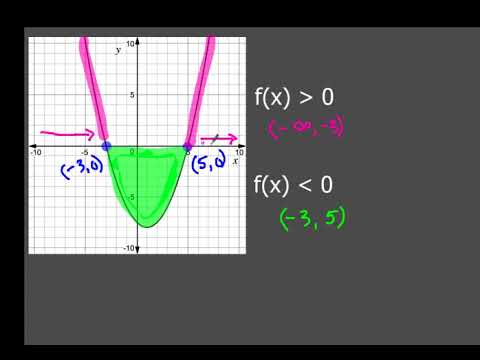
How to tell where f(x) greater than 0 or f(x) less than 0 How to tell where f(x) greater than 0 or f(x) less than 0If f''(x) >0 on an interval, then f is concave upward on that interval d) If f''(x)A key observation is that a sentence like f(x) =0 f ( x) = 0 or f(x) >0 f ( x) > 0 is a sentence in one variable, x x To solve such a sentence, you are looking for value (s) of x x that make the sentence true The function f f is known, and determines the graph that you'll be investigating



3



Local Extrema Of Functions
Get the free "Solve f(x)=0" widget for your website, blog, Wordpress, Blogger, or iGoogle Find more Mathematics widgets in WolframAlphaAnswer and Explanation 1 When presented with the information that f(x) = 2, f ( x) = 2, this means that there exists some function where some input x x produces an output f(x), f ( x), and thatF (x,y)=0 is a two variable function where x and y are variables whereas in the second and third cases they are single variable functions and here we are simply substituting the xy and x/y in the function f 585 views




For The Following Exercises Use The Mean Value Chegg Com




Big O Notation Wikipedia
Summary "Function Composition" is applying one function to the results of another (g º f) (x) = g (f (x)), first apply f (), then apply g () We must also respect the domain of the first function Some functions can be decomposed into two (or more) simpler functionsIf x is close enough to 0 For the formal definition, suppose f(x) and g(x) are two functions defined on some subset of the real numbers We write f(x) = O(g(x)) (or f(x) = O(g(x)) for x> to be more precise) if and only if there exist constants N and C such that First let's find the derivative f ′ ( x) = 3 x 2 4 x − 1 f ′ ( x) = 3 x 2 4 x − 1 Now, to find the numbers that satisfy the conclusions of the Mean Value Theorem all we need to do is plug this into the formula given by the Mean Value Theorem



Max And Min S



Www3 Nd Edu Apilking Math Calc1lectures Lecture 3 limits Pdf
P ( X > x a X > a) = P ( X > x) If X is exponential with parameter λ > 0, then X is a memoryless random variable, that is P ( X > x a X > a) = P ( X > x), for a, x ≥ 0 From the point of view of waiting time until arrival of a customer, the memoryless property means that it does not matter how long you have waited so far If you Answers and Replies is the amplitude of a sinusoidal forcing function, is the undamped natural frequency of the system, and is the frequency of the forcing function, which looks something like or The definition of shown is also the damped natural frequency of the system So are the units for F_0 meters?Hence, the name "piecewise" function When I evaluate it at various x values, I have to be careful to plug the argument into the correct piece of the function




Match The Conditions F X Less Than 0 And F X Less Than 0 With One Of The Graphs In The Figure Study Com



What Is The Meaning Of Math F X 0 Math And Math F X 0 Math Quora
A function f f f is differentiable at a point x 0 x_0 x 0 if 1) f f f is continuous at x 0 x_0 x 0 and 2) the slope of tangent at point x 0 x_0 x 0 is well defined At point c c c on the interval a, b a, b a, b of the function f (x) f(x) f (x), where the function is continuous on a, b a, b a, b, there is a To break it down to its components, let's define each part of the formula Y the outcome or outcomes, result or results, that you want X the inputs, factors or whatever is necessary to get the outcome (there can be more than one possible x) F the function or process that will take the inputs and make them into the desired outcome Simply put, the Y=f(x) equationFor example, if f is a function that has the real numbers as domain and codomain, then a function mapping the value x to the value g(x) = 1 / f(x) is a function g from the reals to the reals, whose domain is the set of the reals x, such that f(x) ≠ 0 The range of a function is the set of the images of all elements in the domain
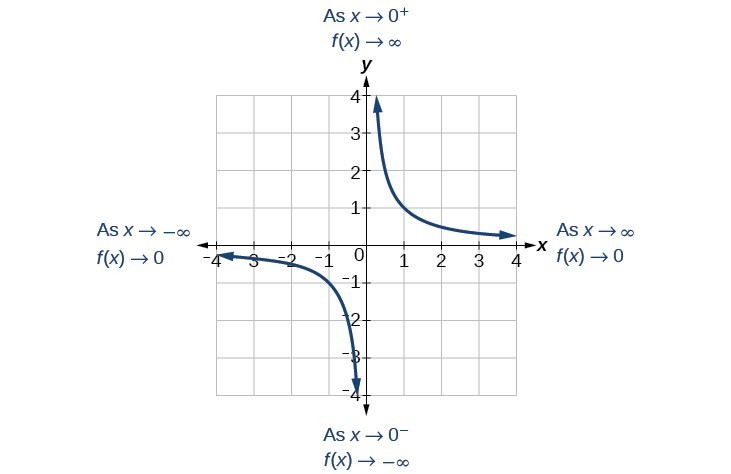



Use Arrow Notation College Algebra
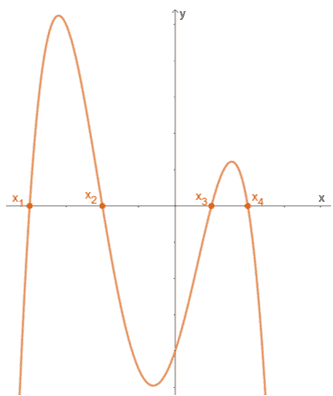



Zeros Of A Function Explanation And Examples
But, I still need t0 understand this in term of mean value theorem So here it goes Suppose f is differentiable on ( 0, ∞) and lim x → ∞ f ′ ( x) = 0 Prove that lim x → ∞ f ( x 1) − f ( x) = 0 Here, can we assume f ′ ( x) = f ( x 1) − f ( x) ( x 1) − x and proceed to conclusion?18B Local Extrema 2 Definition Let S be the domain of f such that c is an element of S Then, 1) f(c) is a local maximum value of f if there exists an interval (a,b) containing c such that f(c) is the maximum value of f on (a,b)∩S 2) f(c) is a local minimum value of f if there exists an interval (a,b) containing c such that f(c) is the minimum value of f on (a,b)∩S 3) f(c) is a local In order to find what value (x) makes f (x) undefined, we must set the denominator equal to 0, and then solve for x f (x)=3/ (x2);
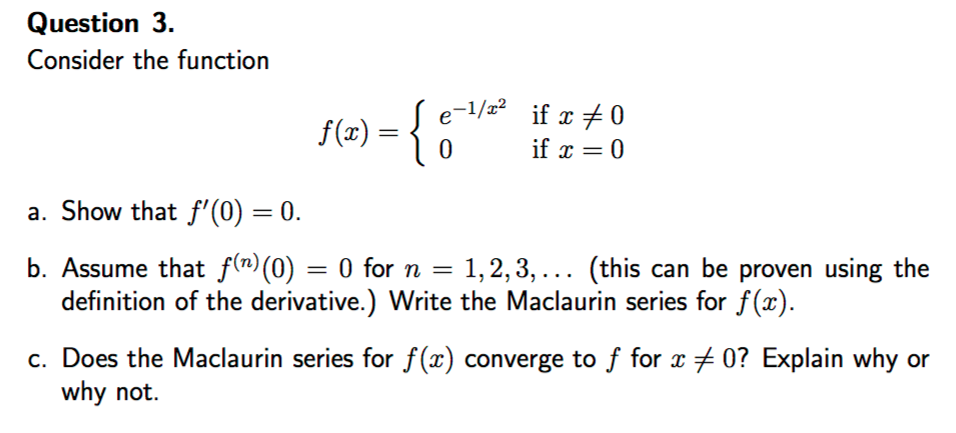



Consider The Function F X E 1 X 2 If X 0 0 If Chegg Com




Define The Real Valued Function F R 0 Gt Rdefined By F X 1 X X In R 0 Complete The Table Given Below Using This Definition What Is The Domain And Range Of This Function Y 1 X
The functions f(x) and g(x) are defined as f(x) = 3x 1 and g(x) = 4x 2 fog(x) = f(g(x)) = f(4x 2 ) = 3(4x 2) 1 = 12x 6 1 = 12x 7 fog(0) = 12*0 7 = 7Chapter 2 21 Functions definition, notation A function is a rule (correspondence) that assigns to each element x of one set , say X, one and only one element y of another set, Y The set X is called the domain of the function and the set of all elements of the set Y that are associated with some element of the set X is called the range of the functionF (x) basically means y, and f' (x) means dy/dx The x can have a value, so for example, f (x) = 2x 1, then f (1) = 3 that is as good as I can explain it!!!




Why Does The Theta 1 Theta F Y F X G X G Y Le 0 Means Both F And G Are Increasing Or Decreasing Mathematics Stack Exchange




The Function F Is Defined By F X 4x2 5x 1 The Chegg Com
The zero of a function is the xvalue that, when plugged into a function, makes the function equal to 0 f (x) means that we have a function of x The zero of the function f (x)=2x2 is the xvalue that makes f (x) = 0 So we can just set the function equal to 0, and then solve for x! The derivative of f (x) f ( x) with respect to x is the function f ′(x) f ′ ( x) and is defined as, f ′(x) = lim h→0 f (x h)−f (x) h (2) (2) f ′ ( x) = lim h → 0 f ( x h) − f ( x) h Note that we replaced all the a 's in (1) (1) with x 's to acknowledge the fact that the derivative is really a function as wellF(x) = (sinx)/x An approximate graph is indicated below Looking at the graph, it is clear that f(x) ≤ 1 for all x in the domain of f Furthermore, 1 is the smallest number which is greater than all of f's values o y=(sin x)/x 1 Figure 1 Loosely speaking, one might say that 1 is the 'maximum value' of f(x)




Define The Real Valued Function F R 0 Gt Rdefined By F X 1 X X In R 0 Complete The Table Given Below Using This Definition What Is The Domain And Range Of This Function Y 1 X
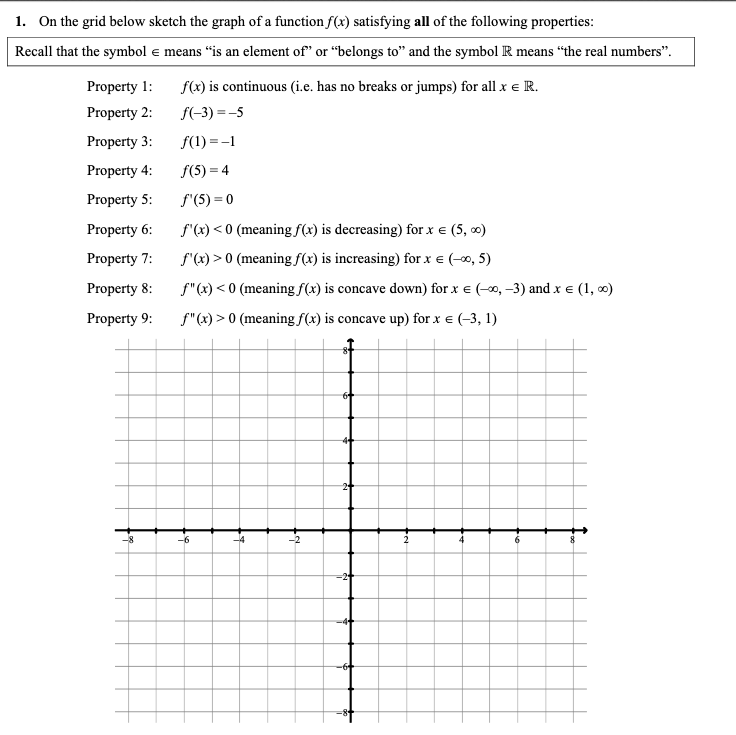



1 On The Grid Below Sketch The Graph Of A Function Chegg Com
It says, for example, that if x< 0, then f' (x)> 0 The derivative, f' (x), can be interpreted as "the slope of the tangent line" f' (x)> 0 means all tangent lines have positive slope are going up to the right Also "if x> 0, then f' (x)< 90" so for x positive, the derivative is negative which means tangent lines are going down to the right17 Inverse Functions Notation The inverse of the function f is denoted by f 1 (if your browser doesn't support superscripts, that is looks like f with an exponent of 1) and is pronounced "f inverse" Although the inverse of a function looks like you're raising the function to theBy the derivative of a function f (x), we mean the following limit, if it exists We call that limit the function f ' (x) " f prime of x " and when that limit exists, we say that f itself is differentiable at x, and that f has a derivative And so we take the limit of the difference quotient as h approaches 0




Graph Domain And Range Of Absolute Value Functions




Question Video The Mean Value Theorem Nagwa
8x 0 2dom(f);8v2Rn and 8 st x 0 v2dom(f)Hence, fis convex i >>>is the unsigned bitwise rightshift operator 0x0F is a hexadecimal number which equals 15 in decimal It represents the lower four bits and translates the the bitpattern 0000 1111& is a bitwise AND operation (x >>> 4) & 0x0F gives you the upper nibble of a byte So if you have 6A, you basically end up with 06 6A = ((0110 1010 >>> 4) & 0x0F) = (0000 0110 & 0x0F) =Given the function f (x) as defined above, evaluate the function at the following values x = –1, x = 3, and x = 1 This function comes in pieces;




Quadratic Example For What Values Of X Is F X Greater Than 0 Youtube



Critical Points
The first derivative of a function See calculus These cookies may be set through our site by our advertising partners They may be used by those companies to build a profile of your interests and show you relevant adverts on other sites




Derivative Of Exponential Function What Does This Text Mean Mathematics Stack Exchange



3 4 The Mean Value Theorem Mathematics Libretexts



Limits And Derivatives Ppt Download




Problem 2 Find O Satisfying The Mean Value Theorem For F X On The Interval 0 1 Homeworklib




Does The Function Satisfy The Mean Value Theorem F X X 3 X 1 0 2 Find Numbers C Satisfy Youtube




Prove That If F X 0 On An Interval A B On A For A Differentiable Function F Then F Is One To One On A Mathematics Stack Exchange




It X 1 Consider The Function F X Y Ja2 0 If Chegg Com



Calc 1 F X 0 If X 0 What Does This Mean Physics Forums



How To Tell Where F X Is Less Than 0 Or Greater Than 0 Youtube



Domain And Range



Inflection Points
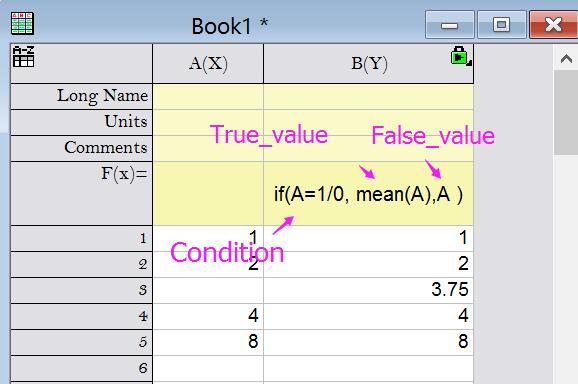



Help Online Quick Help Faq 871 Does Origin Have A If Function



Users Math Msu Edu Users Magyarp Math132 Notes 3 2 Mean Value Theorem Pdf
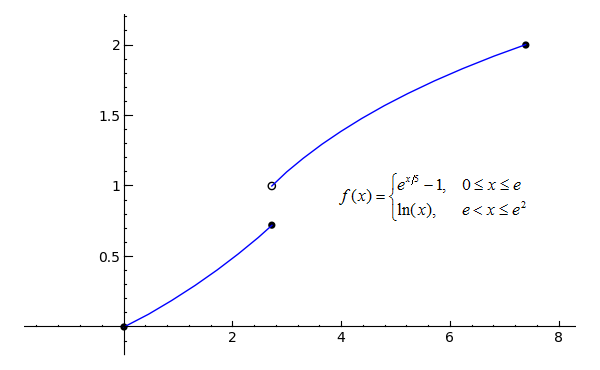



Sage Calculus Tutorial Continuity




The Function F X X 0 Lessthanorequalto X 1 0 Chegg Com




Justification With The Mean Value Theorem Table Video Khan Academy




Limits




Ex 5 8 3 If F X Is Differentiable And F X Does Not Vanish
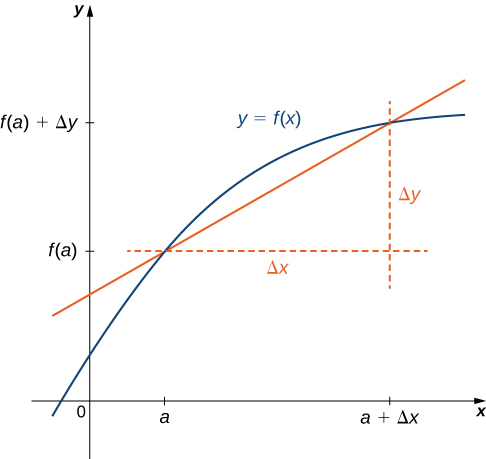



3 2 The Derivative As A Function Mathematics Libretexts




Let F X Be Defined In 0 1 Then The Domain Of Definition Of F E X F In X Is Youtube




If F X Satisfies The Requirements Of Lagrange S Mean Value Theorem On 0 2 And If F 0 0 An Youtube




Definition Of A Logarithmic Function For X 0 And B 0 B 1 Y Log B X Is Equivalent To B Y X The Function F X Log B X Is The Logarithmic Function Ppt Download




Example 15 F X 1 X What Is The Domain And Range Examples




Ex Determine The Sign Of F X F X And F X Given A Point On A Graph Youtube




Answered If F X 3x Sin 47x For X E 0 Bartleby




Meaning Of The Notation Mathcal F X F X Mathematics Stack Exchange
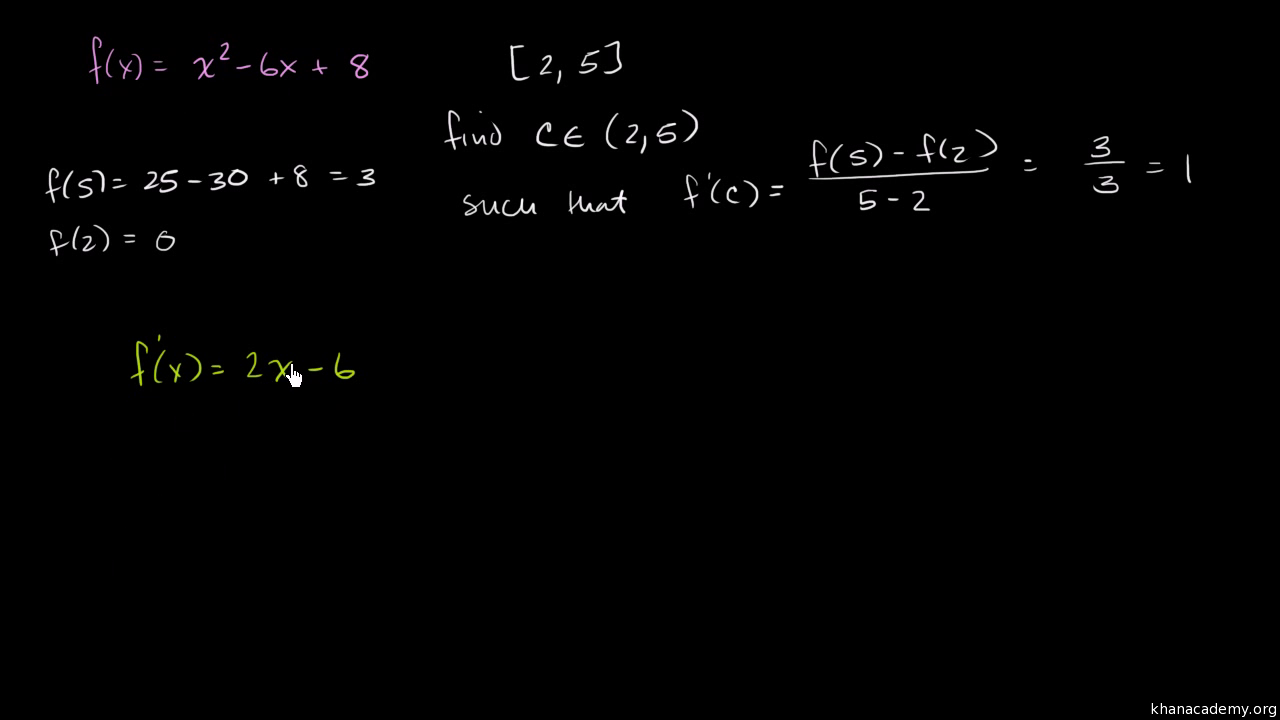



Mean Value Theorem Example Polynomial Video Khan Academy
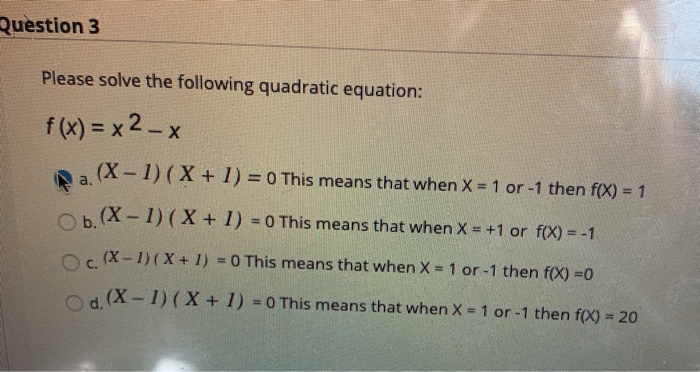



Question 3 Please Solve The Following Quadratic Chegg Com




Solve F X Less Than 0 Where F X X 2 X 3 Youtube




The Derivative



Answered Explain Why The Condition Of A 0 Is Bartleby



Www Shsu Edu Kws006 Precalculus 1 2 Function Graphs Files S 26z 1 6 Pdf




Derivative Wikipedia
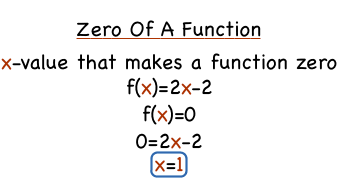



What S The Zero Of A Function Virtual Nerd




Ex 5 8 5 Verify Mean Value Theorem F X X3 5x2 3x




Answered 15 F X Vx 0 4 16 F X X Bartleby




One To One Functions And Their Inverses Ck 12 Foundation




What Is The Difference Between Y F X And Y F X Quora




The Definition Of The Derivative Wolfram Demonstrations Project



Http Cneacs Weebly Com Uploads 2 4 8 5 2 Sec 4 2 Mean Value Theorem Pdf



Increasing And Decreasing Functions




The Average Or Mean Value Of A Continuous Function F X Y Z Over A Solid G Is Defined As F Ave Frac 1 V G Iiint G F X Y Z Dv Where V G Is The




If Lim X To A F X L Is The Value Of L A Function Of A Mathematics Stack Exchange
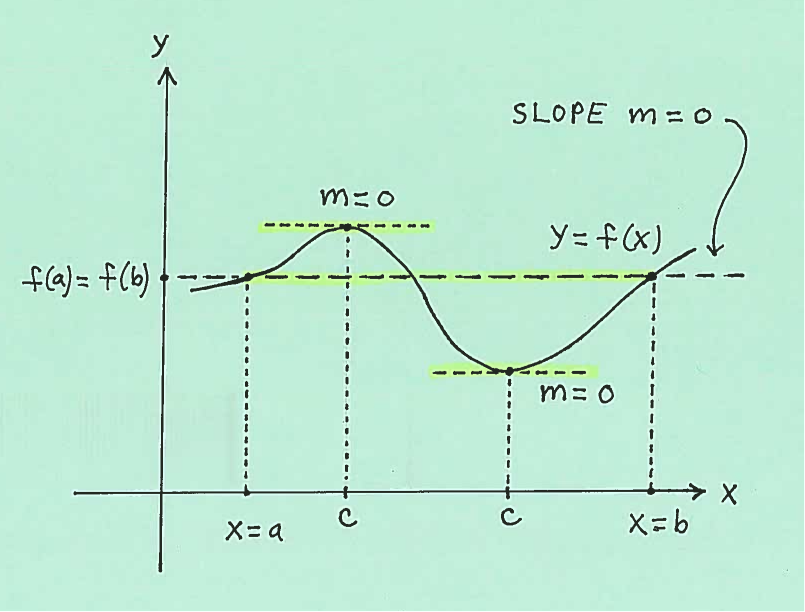



Mean Value Theorem Problems




Verify Lagrange S Mean Value Theorem For The Following Functions In The Given Intervals F X Youtube



What Is The Meaning Of Math F X 0 Math And Math F X 0 Math Quora



Calculus The Definition Of The Derivative



What Does F 0 Represent On The Graph Of F X Quora
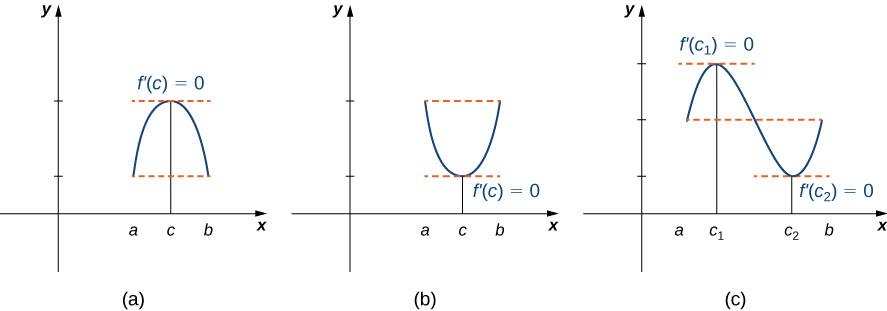



4 2 The Mean Value Theorem Mathematics Libretexts
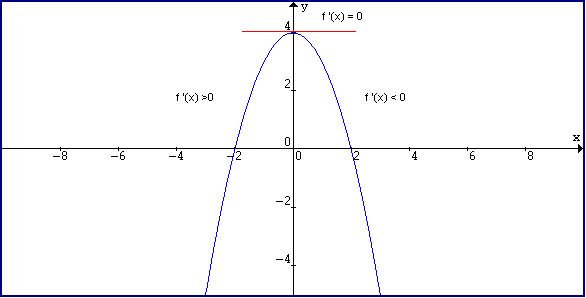



Derivative And Tangent Line



Graphs Of Functions



Interval Notation



1



Limit Definition Of A Derivative




9 F X X4 8x On 0 2 Determine Whether The Mean Chegg Com
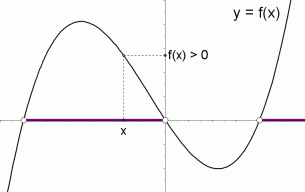



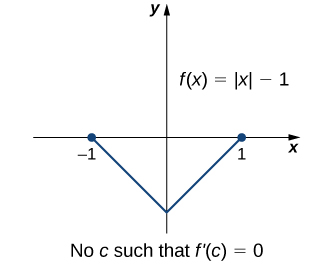
Graphical Interpretation Of Sentences Like F X 0 And F X 0




Mean Value Theorem Video Khan Academy




If F X 0 At Each Point X Of An Open Interval A Chegg Com
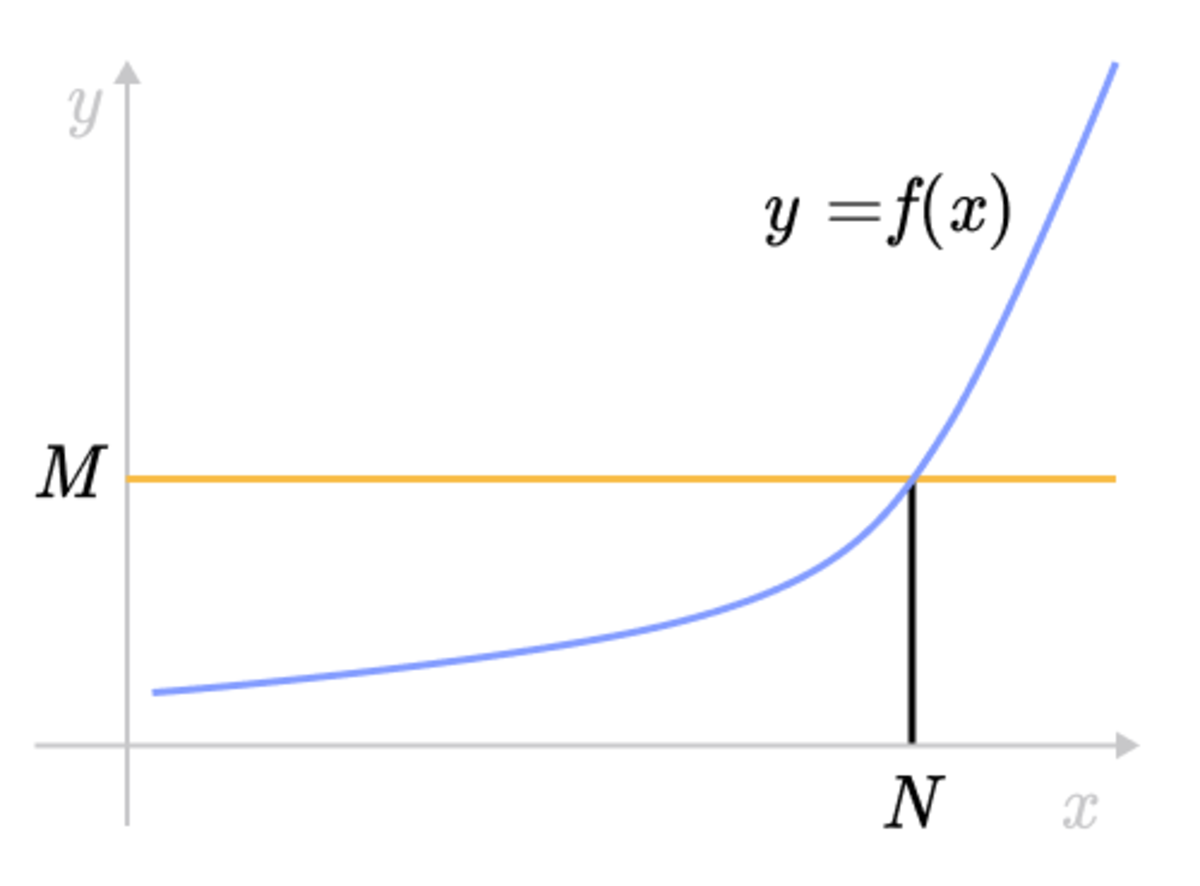



Epsilon Delta Definition Of A Limit Brilliant Math Science Wiki




Property Of The Little O Notation In Calculus Apostol Mathematics Stack Exchange




1 Use The Definition Of The Derivative A Let F X Chegg Com
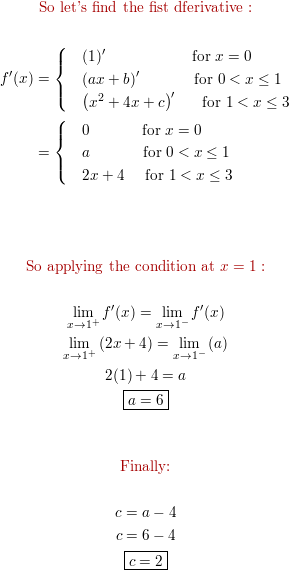



Determine The Values A B And C Such That The Function F Satisfies The Hypotheses Of The Mean Value Theorem On The Interval 0 3 F X 1 X 0 Ax B



Www hs Boone K12 Ky Us Userfiles 531 Classes 9731 Quiz key Pdf Id



Inflection Points
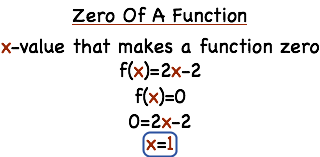



What S The Zero Of A Function Printable Summary Virtual Nerd




Example Find The Derivative Of The Function F X Chegg Com




Extrema Of A Function




Xy X2 If X Y 0 0 Consider The Function F X Y Chegg Com
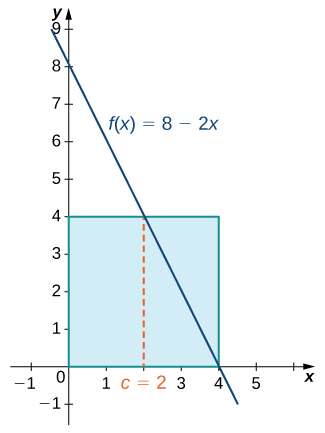



5 3 The Fundamental Theorem Of Calculus Calculus Volume 1
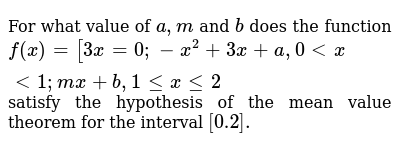



For What Value Of A M And B Does The Function F X 3 X 0 X 2 3x A 0 X 1 Mx B 1 X 2satisfy The Hypothesis Of The Mean Value



Solution It Says Quot Find F X 0 Quot What Does It Mean The Porblem F X 3x 12
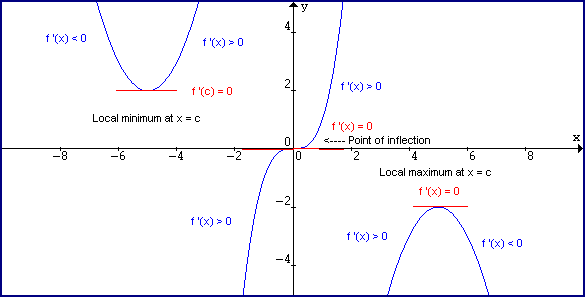



Derivative And Tangent Line
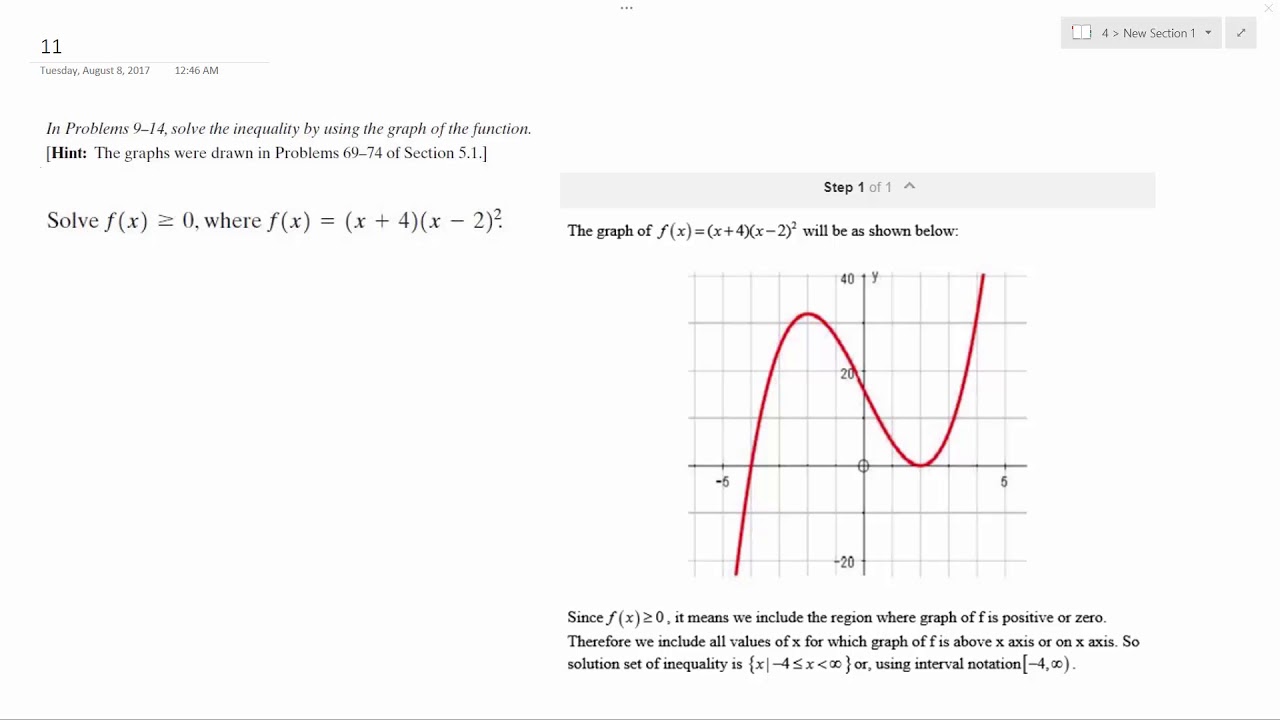



Solve F X Greater Than 0 Where F X X 4 X 2 2 Youtube
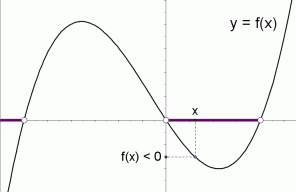



Graphical Interpretation Of Sentences Like F X 0 And F X 0




I Didn T Understand The Below From Sets And Functions Algebra Caltech Pdf The Highlight Is My Problem What Does It Mean And Why Does Say X 0 Mathematics Stack Exchange



What Is The Meaning Of Math F X 0 Math And Math F X 0 Math Quora
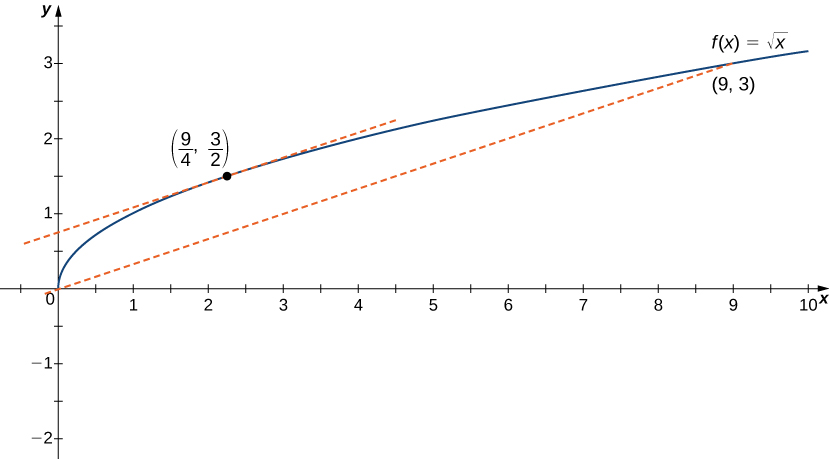



4 4 The Mean Value Theorem Calculus Volume 1



1



0 件のコメント:
コメントを投稿